算法导论其二:分治
目录
分治法是诸多算法的基本思想,把大问题分解为小问题,依次解决并最终合并。
经典案例
-
二分查找
- 对有序序列查找指定元素:
- 比较序列中间元素和目标值
- 递归查找左侧、右侧
- 找到时直接返回
- 代码(C++)
// std::upper_bound(首个大于value)可能的实现 template<class ForwardIt, class T> ForwardIt upper_bound(ForwardIt first, ForwardIt last, const T& value) { ForwardIt it; typename std::iterator_traits<ForwardIt>::difference_type count, step; count = std::distance(first,last); while (count > 0) { it = first; step = count / 2; std::advance(it, step); //替换为if(*it<value) 则是lower_bound(首个不小于value) if (!(value < *it)) { first = ++it; count -= step + 1; } else { // 这里需要理解,虽然看起来当前*it被排除在范围外了,但仍可能是最终结果 count = step; } } return first; } - 时间复杂度:$T(n)=T(n/2)+\Theta(1)$ 也即 $T(n)=\Theta(logn)$。
- 对有序序列查找指定元素:
-
快速幂运算
- 求x的n次方
- 求$x^{\frac{n}{2}}$次方
- 求$x^{\frac{n}{2}} * x^{\frac{n}{2}}$
- 代码(C++)
int pow(int x, int n){ int result = 1; // 自底向上非递归写法(其实用在这里是一个不恰当的例子) // 但本写法是最好的写法,从二进制角度好理解一些 while (n != 0) { if (n & 1) { result *= x; } x *= x; n >>= 1; } return result; }
- 求x的n次方
-
斐波那契数列
- 暴力的自顶向下是指数时间复杂度的$O(\phi^n)$
- 带备忘录的自顶向下,或者递推式的自底向上是线性时间复杂度的$O(n)$
- 斐波那契数列通项公式(利用快速幂运算),可以达到$O(logn)$
- 通项公式:$Fib(n)=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n]$
-
矩阵快速幂
- 用通项公式求解斐波那契数列有一个致命的问题,浮点数运算是有误差的
- 实际上斐波那契数列可以用矩阵乘法表示
- $\left(\begin{matrix} f_{n+1} & f_{n} \\ f_{n} & f_{n-1} \\ \end{matrix}\right) = \left(\begin{matrix} 1 & 1 \\ 1 & 0 \\ \end{matrix}\right)^n$
- 依然可以用快速幂的思路分治递归
-
Strassen算法
- 两个$n$阶方阵相乘,最直接的算法是$O(n^3)$。
- 错误的分治尝试:
- 将矩阵分块 $\left(\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{matrix}\right) = \left(\begin{matrix} B_{11} & B_{12} \\ B_{21} & B_{22} \\ \end{matrix}\right)\left(\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \\ \end{matrix}\right)$
- $A_{11}=\left(\begin{matrix} B_{11} & B_{12} \end{matrix}\right) \left(\begin{matrix} C_{11} \\ C_{21} \end{matrix}\right)$ 同理其他…
- 因为将大矩阵分为4块,每一块需要执行2次矩阵乘法和一次矩阵加法,复杂度为$T(n)=8O(n/2)+O(n^2)$,由主定理可知$T(n)=\Theta(n^3)$
- 问题在于子问题数量8仍然太大(子问题的乘法数量太多了)
- 正确的分治尝试:
- $P_1=A_{11} * (B_{12}-B_{22})$
- $P_2=(A_{11}+A_{12})*B_{22}$
- $P_3=(A_{21}+A_{22})*B_{11}$
- $P_4=A_{22}*(B_{21}-B_{22})$
- $P_5=(A_{11}+A_{22})*(B_{11}+B_{22})$
- $P_6=(A_{12}-A_{22})*(B_{21}+B_{22})$
- $P_7=(A_{11}-A_{21})*(B_{11}+B_{12})$
- $A_{11}=P_5+P_4-P2+P6$
- $A_{12}=P_1+P_2$
- $A_{21}=P_3+P_4$
- $A_{22}=P_1+P_5-P3-P7$
- 复杂度(计算$P_1$到$P_7$7个子问题)$T(n)=7(n/2)+O(n^2)=\Theta(n^{log_2^7})$
-
H layout(了解)
- 大规模集成电路(VLSI)中希望获得效率尽量高的布局。可认为电子器件往往是成二叉树树形拓扑的,如何尽量减少布局面积。
- 面积=宽×高,可以把递归树的高度和宽度视为面积中的高和宽。
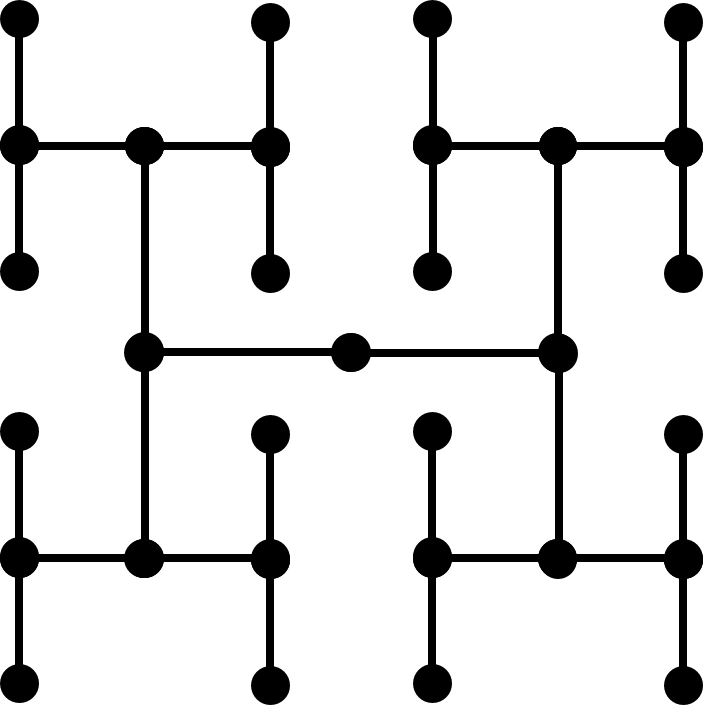
- 一种较优化的解的面积是线性的(n个节点),即H布局,水平和垂直方向,复杂度都是$T(n)=2(n/4)+O(1)=\Theta(\sqrt{n})$。
参考资料
- 部分代码来自于CppReference
本章博客搭建中的坑
- Markdown对\有转义,所以在公式编辑里面矩阵换行的\\则需要打\\\\
